Anyone know math?

"YSI-what can brown do for you" (ysi-what-can-brown-do-for-you) 08/22/2013 at 21:09 • Filed to: None

0

26

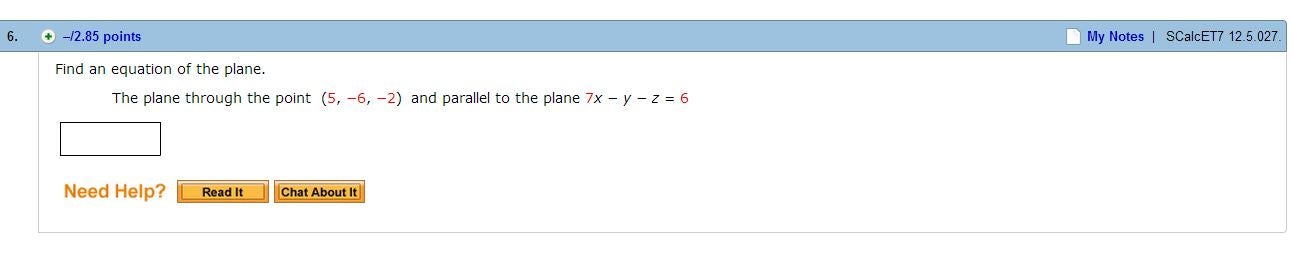
The homework was really easy besides this problem. . . mostly because I can't find it in the book and the professor hasn't taught it yet. So does anyone know what exactly to do?

Leadbull > YSI-what can brown do for you 08/22/2013 at 21:13

1

Copy/paste it into yahoo answers.

No, seriously.

-Amateur > YSI-what can brown do for you 08/22/2013 at 21:14

0

ahhh, I used to know it. With all my classes, I just learn it until the finals and then it's like a memory wipe. Only have a year left and I'll be done with college. I worry about future me when I get a real job in Finance...I'm not going to remember anything .

BlazinAce - Doctor of Internal Combustion > YSI-what can brown do for you 08/22/2013 at 21:15

0

I used to... Math has always been a huge advantage in Vestibular exams in Brazil, so that stuff was pretty much required, but nowadays I don't even remember what it's called. Analytic Gemometry? I believe that's what they called it here...

YSI-what can brown do for you > Leadbull 08/22/2013 at 21:24

0

Nothing comes up beside a bunch of books. No concrete examples.

YSI-what can brown do for you > BlazinAce - Doctor of Internal Combustion 08/22/2013 at 21:25

0

Geometry? This is Mutlivariable Calculus. . . although pretty simple stuff WHEN the proffesor explains it too you.

The WB > YSI-what can brown do for you 08/22/2013 at 21:27

0

The normal vector n for the plane is < 7, -1, -1 >. The general equation is:

n (dot product) < x - xo, y - yo, z - zo > = 0

< 7, -1, -1 > (dot product) < x-5, y+6, z+2 >

3( x - 5 ) - 1( y + 6 ) - 1(z + 2) = 0

3x - 15 - y - 6 - z - 2 = 0

3x - y - z = 23

If I'm remembering right.

YSI-what can brown do for you > The WB 08/22/2013 at 21:32

0

Okay hold step back a second. How did you get the normal vector? I have been trying to figure that out for about 30 minutes!

The equation you wrote down was right: n(r-ro), I just need to figure out n. . . which was impossible. Also don't you mean 7(x-5) not 3(x-5)?

Leadbull > YSI-what can brown do for you 08/22/2013 at 21:32

2

Oh, dang. I literally did all my Chem. homework that way.

Also, Wolfram Alfa is great.

Buick Mackane > YSI-what can brown do for you 08/22/2013 at 21:33

0

This post is going to give me nightmares about High School and algebra all over again.

YSI-what can brown do for you > Leadbull 08/22/2013 at 21:34

0

Math is one of my better subjects, just as long as I know the material, right now the teacher hasn't thought us half of this problem.

YSI-what can brown do for you > Buick Mackane 08/22/2013 at 21:34

0

Just be glad you didn't take Calc.

The WB > YSI-what can brown do for you 08/22/2013 at 21:35

1

Ah crap, yes, 7, not 3. Final should be 7x - y - z = 43

Normal vector is straight from the equation of the plane you gave. 7x - y - z. < 7, -1, -1>

YSI-what can brown do for you > The WB 08/22/2013 at 21:38

0

wait. . . what. . . really? I must have been seriously overthinking this problem. One final question I swear. So if they give you the equation for a plane, the normal vector is just the coefficients in front of the variable?

The WB > YSI-what can brown do for you 08/22/2013 at 21:44

0

As far as I understand it yes. The definition of the equation of the normal vector to any plane ax + by + cz + d =0 is just < a, b, c > Remember that d is a constant and can be moved to the other side of the equation (in your example, d is -6)

From Wolfram Alpha: http://mathworld.wolfram.com/NormalVector.h…

MrGuy > YSI-what can brown do for you 08/22/2013 at 21:45

0

To make a new plane that is parallel to the old plane, it has to have the same coefficients on the x, y, z terms in the equation as the old plane, so you have 7x-y-z=K(eq. 1). To make a plane that passes through that point, you take eq. 1 and see what value of K you need to have a plane that passes through (5,-6, -2). To do this, you substitute that point into eq. 1 and solve for K. This is from my recollection from ~5 years ago, so take it with a grain of salt.

YSI-what can brown do for you > The WB 08/22/2013 at 21:46

0

You sir have taught me my lecture, which took my teacher 50 minutes, in 3 comments,

YSI-what can brown do for you > MrGuy 08/22/2013 at 21:48

0

Well you are close, you have to find the normal vector, and then you use dot formula with <7x,-y,-z> and then you solve for K. . . I didn't know how to find the normal vector.

boxrocket > YSI-what can brown do for you 08/22/2013 at 21:50

0

42. The answer is always 42.

The WB > YSI-what can brown do for you 08/22/2013 at 21:52

1

Glad I could help! Math teachers always make it so hard. They tend to go off on tangents.

( Badum-tiss )

YSI-what can brown do for you > boxrocket 08/22/2013 at 21:53

0

You are surprisingly close. The answer I needed to complete the equation was 43. Also I think I found the answer to life.

YSI-what can brown do for you > The WB 08/22/2013 at 21:54

0

I hate you for making that pun. But out of kindness, I will still thank you.

THAaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaank

you

Agrajag > boxrocket 08/22/2013 at 22:36

0

Beat me to it.

dsigned001 - O.R.C. hunter > YSI-what can brown do for you 08/22/2013 at 23:03

0

Seriously though Wolfram alpha. It's not just that it gives you the answer, it spells it out for you. Even though the answer above is correct, it would be worth putting it in.

YSI-what can brown do for you > dsigned001 - O.R.C. hunter 08/22/2013 at 23:04

0

I am not sure how I would put this into wolfram. Does it work out word problems?

dsigned001 - O.R.C. hunter > YSI-what can brown do for you 08/22/2013 at 23:09

0

Remember to simplify the equation though. Sometimes they'll throw that out there or put it in fractions. It should all come out in the wash, but it's an easy way to lose points.

dsigned001 - O.R.C. hunter > YSI-what can brown do for you 08/22/2013 at 23:25

0

It can work out very simple write problems. I'm using my phone atm, so I can't fiddle with it but i used it to do partial differential equations (not word problems), so you can probably play with it and come up with the answer yourself. It's quite a powerful tool. It's the guys behind siri as well iirc.